介绍
skip list是一个非常优秀的数据结构,插入、删除、查找的复杂度均为O(logN),相对于AVL和 红黑树,跳跃表的实现更加地简单。LevelDB的核心数据结构是用跳表实现。
skip list中各个操作的时间复杂度如下所示:
Operation | Time Complexity
-------------------------------------
Insertion | O(log N)
Removal | O(log N)
Check if contains | O(log N)
Enumerate in order | O(N)
盛大创新院的这篇文章对skip list作了很好的介绍, 建议没有接触过skip list的同学先看一下。既然网络上已经有不错的材料,我就不再浪费时间 做无用功了,本文仅介绍skip list的一个简单实现。
实现
skip list概念是其实很好理解,就是一个普通的链表,链表的每个节点高度不一,节点中更高 的链接指向更远的节点(站得高,看得远?)。在查找的时候,就可以首先通过较高的节点跳过那 些不可能的值,以此加快查找速度。
刚接触skip list,可能会有两个疑惑:
- 如何在各个节点中包含不同数量的链接,即如何实现?
- 在插入和删除节点时,可能会改变多个指针,如何做到?
当然,这也可能是我自己的两个疑惑,带着这两个问题,一起来分析一下skip list的实现。
下面来看第一个问题,如何实现在各个节点中包含不同数量的链接。skip list的初始化代码如下:
#define lgNMax 30
typedef struct STnode* link;
typedef int Item;
tpedef Item Key;
struct STnode{ Item item; link * next; int sz; }
static link head, z; //头结点和尾节点
static int N, lgN; //节点总数和skip list当前的高度
link NEW(Item item, int k)
{
int i; link x = malloc(*x);
x->next = malloc(k * sizeof(link));
x->item = item; x->sz = k;
for (i = 0; i < k; i++) x->next[i] = z;
return x;
}
void STinit(int max)
{
N = 0; lg = 0;
z = NEW(NULL, 0);
head = NEW(NULL, lgNMax + 1)
}
如果只看节点定义,根本没有什么特别之处,这就是一个普通的链表节点的定义。
重点是NEW函数,分析函数代码可知,节点的next不是指向下一个节点,而是指向一个数组,
这个数组中,包含了k个元素, 其中,数组的第1个元素(如head->next[0])
用以发挥了普通链表的作用,指向skip list中的 下一个节点。
数组的第2个元素到第k-1个元素,是skip list所特有的,用以跳过某些节点,
指向离自己更远的节点。
如下图所示:
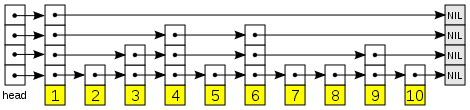
这就回答了上面两个问题的第一个问题。下面来看skip list的查找,因为skip list的查找比较简单, 所以先看查找操作。源码如下:
Item searchR(link k, Key v, int k)
{
if(t == z)return NULL;
if(v == t->item)return t->item;
if(v < t->next[k]->item)
{
if(k == 0)return NULL;
return searchR(t, v, k-1); //向下
}
return searchR(t->next[k], v, k); //向前
}
Item STsearch(Key v)
{ return searchR(head, v, lgN); }
最关键的代码就是有注释的两行代码,完整的步骤如下:
- 当前是否已经到达了skip list的尾部,如果是,则直接返回未找到
- 要找的key是否等于当前节点的值,如果等于,就返回找到
- 没有找到,就需要考虑两种情况。如果要找的key比当前节点小,则向下继续
查找
searchR(t, v, k-1);如果已经到达底部(不能再向下),则返回未找到 - 如果要找的key大于当前节点的key,则向前查找
searchR(t->next[k], v, k)
下面来看插入操作,请忽略randX()函数。
int randX()
{
int i, j, t = rand();
for ( i = 1, j = 2; i < lgNMax; i++, j += j)
if ( t > RAND_MAX/j) break;
if(i > lgN) lgN = i;
return i;
}
void insertR(link t, link x, int k)
{
Key v = x->item;
if( v < t->next[k]->item)
{
if (k < x->sz)
{
x->next[k] = t->next[k];
t->next[k] = x;
}
if ( k == 0 )return;
insertR(t, x, k - 1)return; //向下
}
insertR(t, x, k-1); //向前
}
void STinsert(Item item)
{
insertR(head, NEW(item, randX()), lgN);
N++;
}
在绝大多数数据结构中,做插入操作,将节点插入以后就完事了,但是,前面说过,skip list 可能会修改多个指针。即,skip list中的插入操作,并不是插入以后就完事了, 还需继续向下进行指针的修改。插入过程其实与查找过程非常相似。
要牢记,skip list中的插入操作并不是插入一次以后就完成了,而是到达了节点的底部, 不能再“向下走”以后才结束。这就回答了上面两个问题中的第二个问题, 如何做到一次插入改变多个指针,且每次改变的指针数还不固定。
删除操作与插入操作非常类似,不再赘述。
void deleteR(link t, Key v, int k)
{
l ink x = t->next[k];
i f(x->item > v)
{
if(v == x- >item)
{ t->next[ k] = x->next[ k]; }
if(k == 0)
{ free(x); return; }
deleteR(t, v, k - 1); r eturn;
}
deleteR(t->next[k], v, k);
}
Item STdelete(Key v)
{ deleteR(head, v, lgN); N--; }
本文的skip list实现来自于《算法C语言实现》原书第三版13.5小节。
其他资料:
[1]: Skip lists are fascinating!非递归实现的跳跃表
[2]: leveldb中的skip list 工业界的实现